Pada garis y = mx, m merupakan gradien yang besarnya adalah .
Sekarang, ayo perhatikan garis g pada gambar berikut.
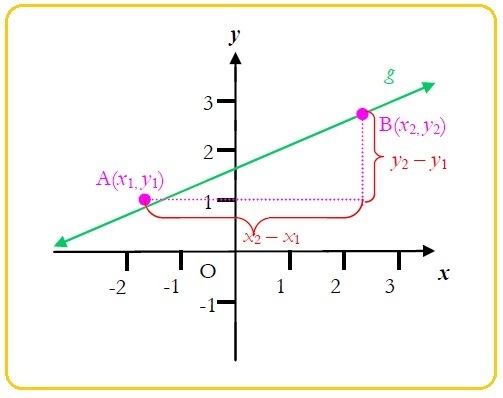
Pada gambar tersebut, dari titik A ke titik B terdapat suatu perubahan secara tegak sebesar y2 – y1 dan perubahan secara mendatar sebesar x2 – x1. Ini menunjukkan garis g yang melalui titik A(x1, y1) dan B(x2, y2) memiliki kemiringan atau gradien sebesar .

Pemahamanmu tentang gradien dapat digunakan untuk mempelajari topik berikut ini.
Pada bagian sebelumnya, kamu telah mengetahui bahwa suatu garis yang melalui titik A(x1, y1) dan B(x2, y2) memiliki gradien . Pada topik sebelumnya, kamu pun telah mempelajari persamaan garis yang melalui titik (x1, y1) dan bergradien madalah y – y1 = m(x – x1).
Dengan mensubstitusi nilai m ke persamaan tersebut, kamu akan mendapatkan:
Dapat disimpulkan bahwa:

Contoh
Ayo, tentukan persamaan garis yang melalui titik (4, 0) dan (0, -2).
Jawab:
Persamaan garis yang melalui titik (4, 0) dan (0, -2) adalah sebagai berikut.
Jadi, persamaan garis yang melalui titik (4, 0) dan (0, -2) adalah x – 2y – 4 = 0.
0 komentar:
Post a Comment