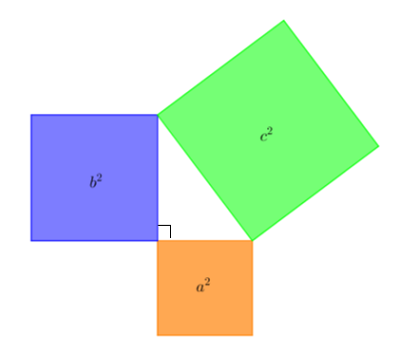
Menentukan Jenis Segitiga jika Diketahui Panjang Sisi-Sisinya Menurut teorema Pythagoras, pada ∆ABC yang siku-siku di C, berlaku c 2 = ...
Read More

Blog Pembelajaran Konsep Matematika SMP | SMA | Olimpiade serta fisika