PERBANDINGAN PANJANG SISI-SISI PADA SEGITIGA KHUSUS 45 45 90

Perhatikan persegi ABCD di bawah ini.

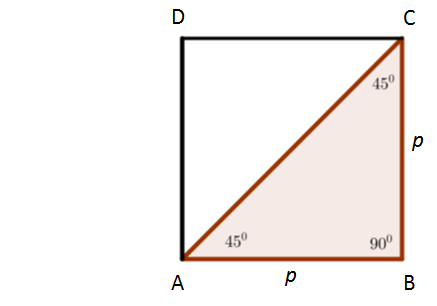
Perhatikan bahwa ABC merupakan segitiga siku-siku sehingga berlaku teorema Pythagoras yaitu,

$\begin{array}{lcl}& A{B}^2+B{C}^2& =A{C}^2\\ \iff & p^2+p^2& =A{C}^2\\ \iff & A{C}^2& =2p^2\\ \iff & AC& =p\sqrt{2}\end{array}$

Perhatikan bahwa $AB:BC:AC=p:p:p\sqrt{2}$ atau $AB:BC:AC=1:1:\sqrt{2}$

Oleh karena,

AB adalah sisi di depan sudut ${45}^{\circ }$ 
BC adalah sisi di depan sudut ${45}^{\circ }$
AC adalah sisi di depan sudut ${90}^{\circ }$

maka kita dapatkan perbandingan berikut.

Perbandingan ini dapat digunakan untuk menyelesaikan soal segitiga siku-siku dengan sudut ${45}^{\circ }$ tanpa menggunakan rumus Pythagoras.

Contoh Soal

Diketahui segitiga PQR siku-siku di P dan besar sudut Q adalah ${45}^{\circ }$. Jika panjang PQ = 7 cm, maka panjang PR dan QR adalah....

Penyelesaian:

Diketahui segitiga PQR siku-siku di P, besar sudut Q = ${45}^{\circ }$, dan panjang PQ = 7 cm.

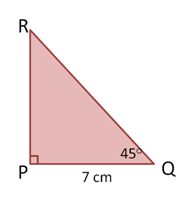
Oleh karena jumlah sudut pada sebuah segitiga = ${180}^{\circ }$, maka besar sudut R = ${180}^{\circ }-({90}^{\circ }+{45}^{\circ })={45}^{\circ }$

Oleh karena segitiga PQR adalah segitiga siku-siku khusus dengan sudut ${45}^{\circ }$, maka berlaku:

$\begin{array}{ccccccccccc}\mathrm{s}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{d}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{p}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{u}\mathrm{d}\mathrm{u}\mathrm{t}{45}^{\circ }& :& \mathrm{s}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{d}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{p}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{u}\mathrm{d}\mathrm{u}\mathrm{t}{45}^{\circ }& :& \mathrm{s}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{r}\mathrm{i}\mathrm{n}\mathrm{g}& =& 1& :& 1& :& \sqrt{2}\\ PQ& :& PR& :& QR& =& 1& :& 1& :& \sqrt{2}\end{array}$.

Selanjutnya diperoleh PQ : PR = 1 : 1 dan PQ : QR = 1 : $2$.

$\begin{array}{llll}& \frac{PQ}{PR}& =& \frac{1}{1}\\ \iff & \frac{7}{PR}& =& \frac{1}{1}\\ \iff & PR& =& 7\times 1\\ \iff & PR& =& 7\end{array}$

$$

$\begin{array}{llll}& \frac{PQ}{QR}& =& \frac{1}{\sqrt{2}}\\ \iff & \frac{7}{QR}& =& \frac{1}{\sqrt{2}}\\ \iff & QR& =& 7\times \sqrt{2}\\ \iff & QR& =& 7\sqrt{2}\end{array}$

Jadi, panjang PR = $7$ dan QR = $7\sqrt{2}$.